BPR算法
最近在学习推荐系统相关的知识,其中用到了贝叶斯推荐模型(Bayesian Personalized Ranking, BPR),故写此文讲讲BPR相关的知识。
BPR模型概念
BPR(Bayesian Personalized Ranking)推荐模型是基于贝叶斯后验优化的个性化排序算法。从user-iem矩阵(即在 用户-物品 这个关系集里找数据)训练出多个矩阵,而且一个矩阵表示一个user对某个item偏好情况来获得其对多个item的偏好关系的推荐系统。本身不优化用户对物品的评分,只是借由评分来优化用户对物品的排序。
简单来说:
- 通过大量不同用户对某几个物体的评价来训练出这几个物体的相似关系。
- 根据某个用户对其中几个物体的评价 与 待评价物体与已评价物体的相似关系,来推算出其对未评价物体的喜好程度。
- 实现推荐。
整个模型的核心是
BPR算法
贝叶斯公式

公式我也理解不深刻,因为我的概率论近似于没学过👴
朴素贝叶斯用于协同过滤
假设我们有一个m*n的矩阵,包含m个用户对n个物品的评价。注意⚠️:这里的评价是隐式评价,比如点击某物品表示喜欢,没点击表示不感兴趣;而不是通过评分分成三六九等。
| 用户\物品 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 1 | -1 | 1 | -1 | 1 | -1 |
| 2 | 1 | 1 | ? | -1 | -1 | -1 |
| 3 | ? | 1 | 1 | -1 | -1 | ? |
| 4 | -1 | -1 | -1 | 1 | 1 | 1 |
| 5 | -1 | ? | -1 | 1 | 1 | 1 |
几个表示方法声明
l 个不同的评分值:
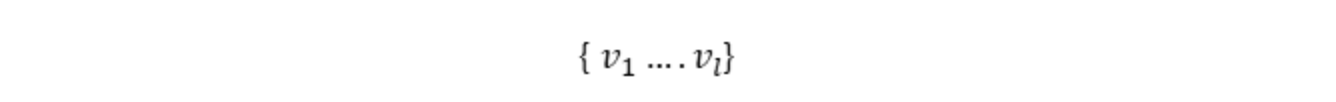
矩阵第 (u, j) 表示:用户 u 对物品 j 的评分。
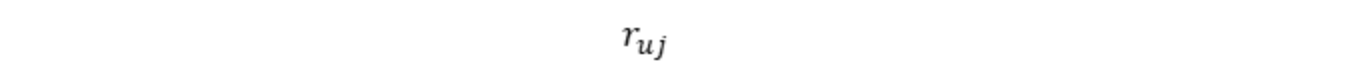
用户 u 已评价物品的评分集合:
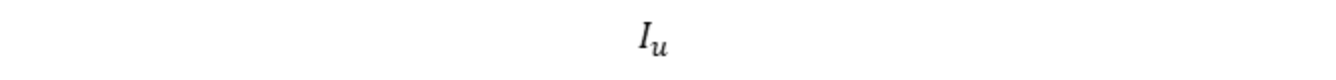
如果用户 u 对物品 1,3,5 有评分:
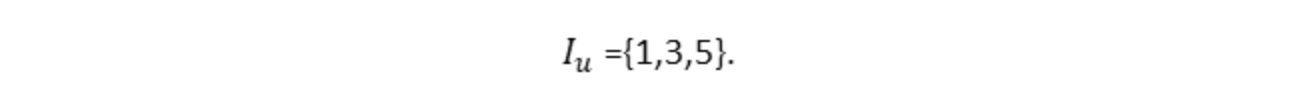
用户 u 对第 j 个物品评分为 vs 的概率:
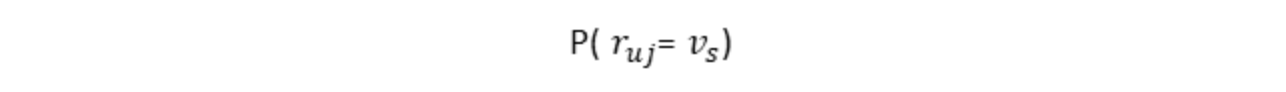
在用户 u 对物品 j 的评分为 vs 的条件下,发生 Iu 的条件概率:

通过对已观测评分 Iu 对 P(ruj = vs) 概率的重新评估:

然后我们就可以通过对 P(ruj=vs | Iu已观测的评分) 进行排序,概率最大的就是用户 u 对物体 j 最有可能的评分,也就是我们的预测。剩下所做的就是对这个公式进行化解,使之方便计算。
最终可以得到朴素贝叶斯协同过滤公式:
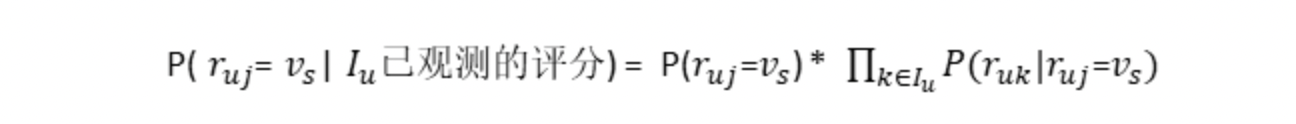
All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.
