这几天疯狂使用Binary Heap，所以打算写篇文章好好整理下这个数据结构。这个结构的 Insert 操作的时间复杂度是 O(n) ，但是他的 DeleteMin 操作能实现 O(1) 。因为完全二叉堆的结构很有规律，所以我们不需要用树结构来实现二叉堆，用数组即可。其中父节点在位置 i 上，左节点在位置 2i 上，右节点在 2i+1 上。

头文件

1
2
3
4
5
6
7
struct HeapStruct
{
    int Capacity;		// 容量
    int Size;				// 当前堆的大小
    int *Elements;	// 元素数组
};
typedef struct HeapStruct *PriorityQueue;

初始化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// MaxElements 是这个堆最大的节点数
PriorityQueue Init(int MaxElements)
{
    PriorityQueue H;
  
  	// 申请空间
    H = (PriorityQueue)malloc(sizeof(struct HeapStruct));
    H->Elements = (int*)malloc((MaxElements+1)*sizeof(int));
    
    H->Capacity = MaxElements;
    H->Size = 0;
    H->Elements[0] = MinData;	// 我在最初定义MinData为-1，这里做一个哑节点用
    
    return H;
}

插入

1
2
3
4
5
6
7
8
9
void Insert(int X, PriorityQueue H)
{
    int i;
  	// 上滤操作
    for(i=++H->Size; H->Elements[i/2]>X; i/=2)
        H->Elements[i] = H->Elements[i/2];
    // 插入操作
  	H->Elements[i] = X;
}

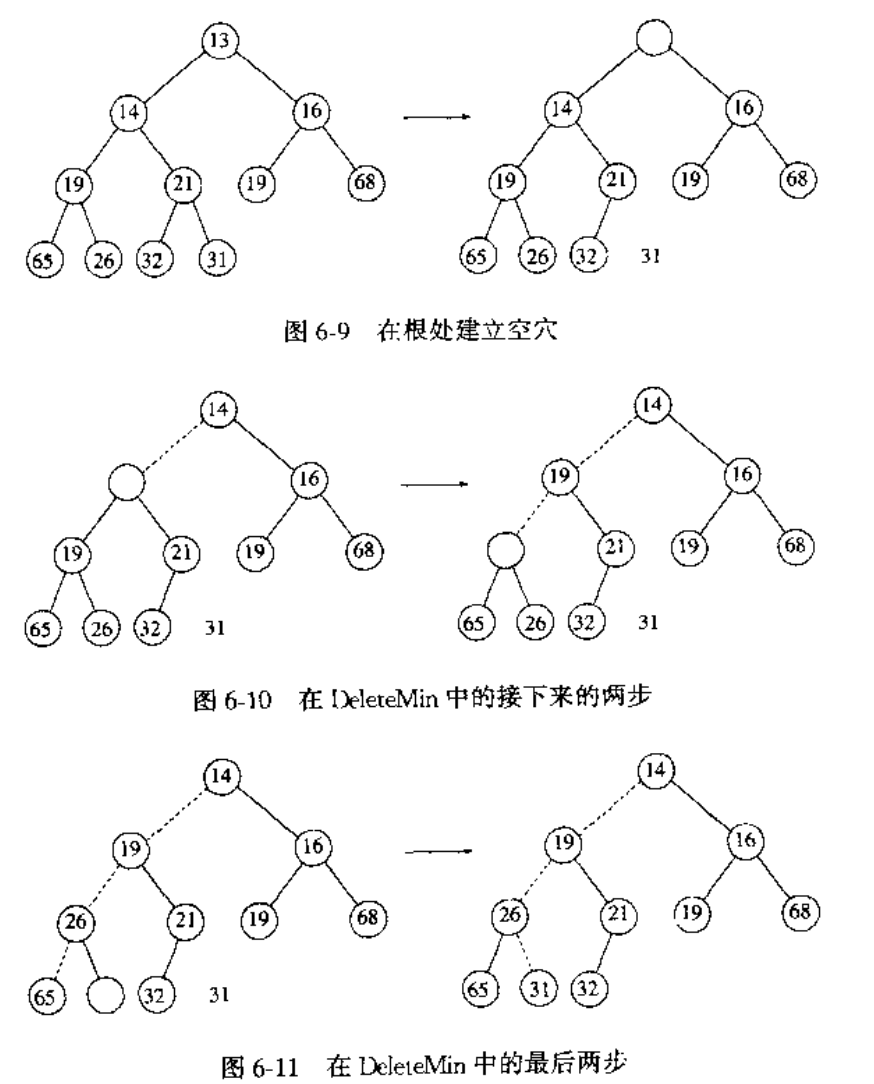
插入的策略是【上滤】。

我们先在堆的下一个可用位置新建一个空穴。比较空穴的父节点与待插入节点的大小。如果父节点比待插入元素小，说明该位置是待插入的位置。反之则将空穴上滤。

1

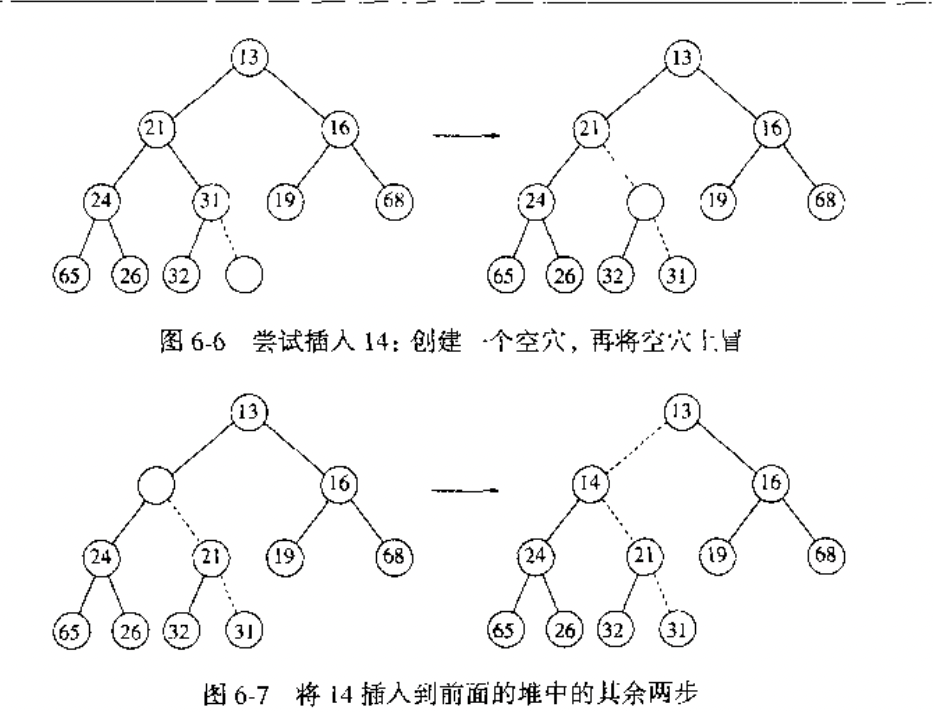
DeleteMin

其实可以看得出，堆的第一个元素就是最小值。所以我们要做的就是，返回第一个元素，然后调整堆结构。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int DeleteMin(PriorityQueue H)
{
    int i, Child;
    int MinElement, LastElement;
    
    MinElement = H->Elements[1];
    LastElement = H->Elements[H->Size--];
    
    // 下滤
  	for(i=1; i*2<=H->Size; i=Child)
    {
        Child = i * 2;
        if(Child != H->Size && \
           H->Elements[Child+1] < H->Elements[Child])
            Child++;
        
        if(LastElement > H->Elements[Child])
            H->Elements[i] = H->Elements[Child];
        else
            break;
    }
  	// 调整最后一个元素到空穴
    H->Elements[i] = LastElement;
    
    return MinElement;
}

这里使用的策略是【下滤】

我们在根节点处建立空穴，往下走，把子节点中较小的节点移到空穴处，直达达到叶节点。然后把堆的最后一个元素放到空穴中。

2