相比Avl Tree，Red-black Tree的操作复杂很多，不过网上优秀的文章也很多。这篇文章参考[简书某博客][https://www.jianshu.com/p/e136ec79235c]

写成的，文章中的配图大部分也是原博客上的。

定义

红黑树需要满足以下四个性质：

  • 每个节点要么是黑色，要么是红色。
  • 根节点是黑色的。
  • 每个叶子节点（NIL）是黑色。
  • 每个红色结点的两个子结点一定都是黑色。
  • 任意一结点到每个叶子结点的路径都包含数量相同的黑结点。

基本操作

和Avl Tree一样，红黑树保持平衡的主要方式有左旋和右旋，同时红黑树还需要新的操作——变色。

假设我们有结构体：

1
2
3
4
5
6
7
8
typedef struct RBNode *RBTree;
struct RBNode
{
  int val;
  RBTree Left;
  RBTree Right;
  int color;
};

左旋

以某个结点作为支点(旋转结点)，其【右子结点】变为旋转结点的【父结点】，【右子结点的左子结点】变为【旋转结点的右子结点】，左子结点保持不变。

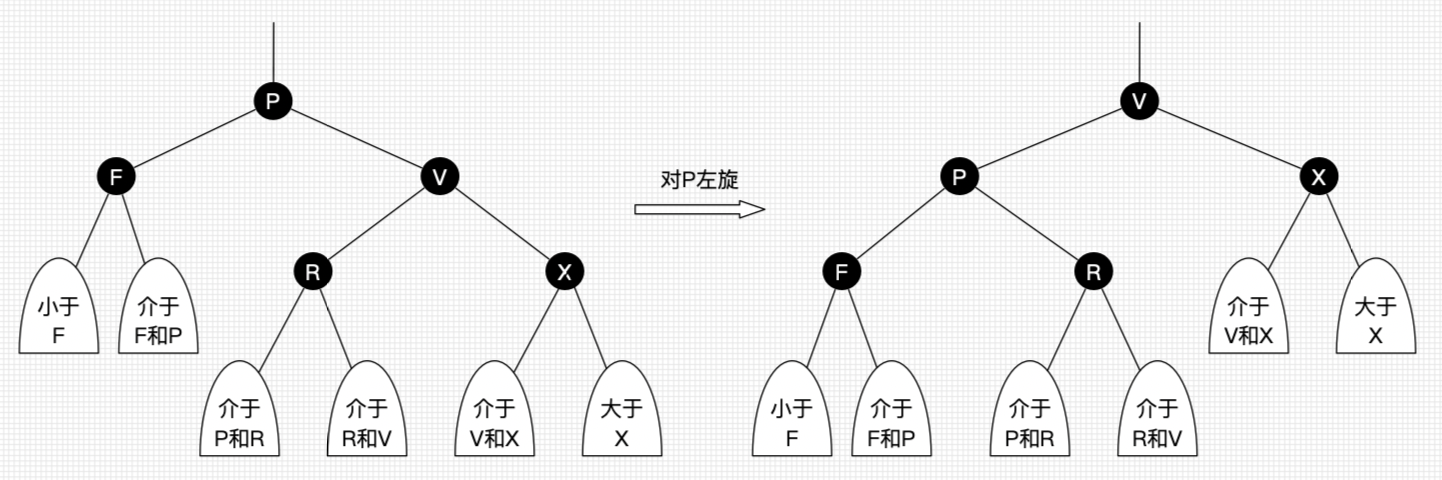
对应代码可以简写为（⚠️：以下代码不涉及变色操作，只是单纯的AVL Tree的旋转）

1
2
3
4
5
6
7
RBTree LeftRotate(RBTree P)
{
  RBTree V = P->Right;
  P->Right = V->Left;
  V->Left = P
  return V;
}

右旋

以某个结点作为支点(旋转结点)，其【左子结点】变为旋转结点的【父结点】，【左子结点的右子结点】变为【旋转结点的左子结点】，右子结点保持不变。

1
2
3
4
5
6
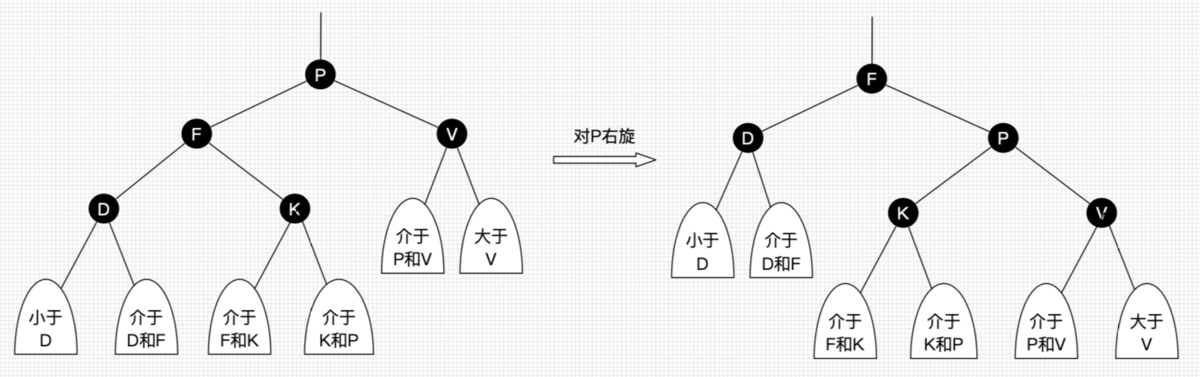
7
RBTree RightRotate(RBTree P)
{
  RBTree V = P->Left;
  P->Left = V->Right;
  V->Right = P
  return V;
}

变色

结点的颜色由红变黑或由黑变红。

红黑树的查找

和二叉树的查找方法一致。

时间复杂度为 O(2lgN)

红黑树的插入

插入主要包括两个工作：

  • 找插入的位置
  • 插入后调整平衡

第一步很简单，就和二叉树的插入操作找位置是一样的。

接下来的部分就是这部分的重点内容了。

调整平衡

首先我们要确定插入节点的颜色都初始化为【红色】，因为红色不会影响整棵树的黑高。那么会出现的不平衡状况就是：父节点是红色时的插入。

情况1: 叔节点存在且为红色

调整方法很简单：黑红红 => 红黑红

情景2: 叔节点不存在或者为黑色

主要分为 SingleRotate 和 DoubleRotate 两种情况。

SingleRotate

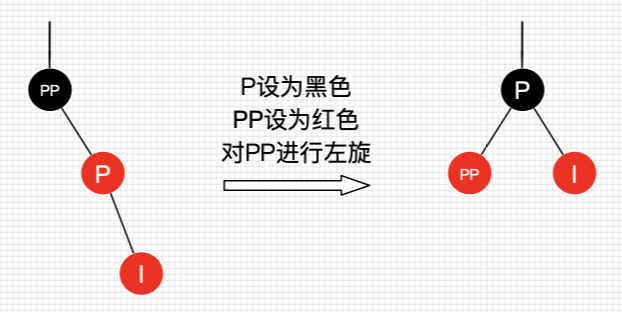
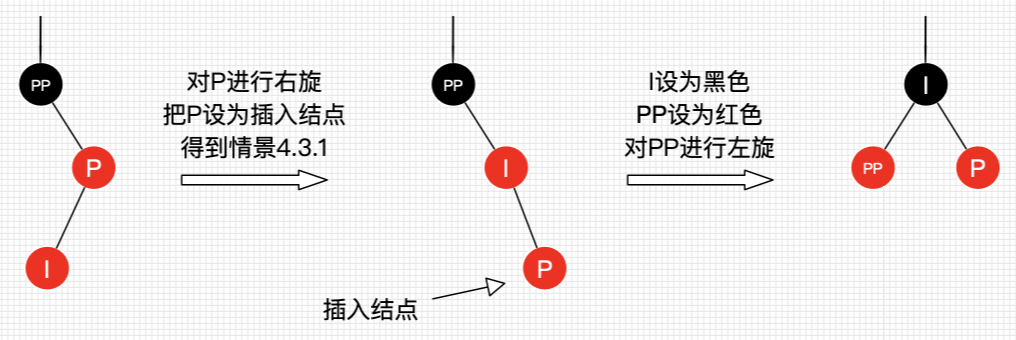
DoubleRotate

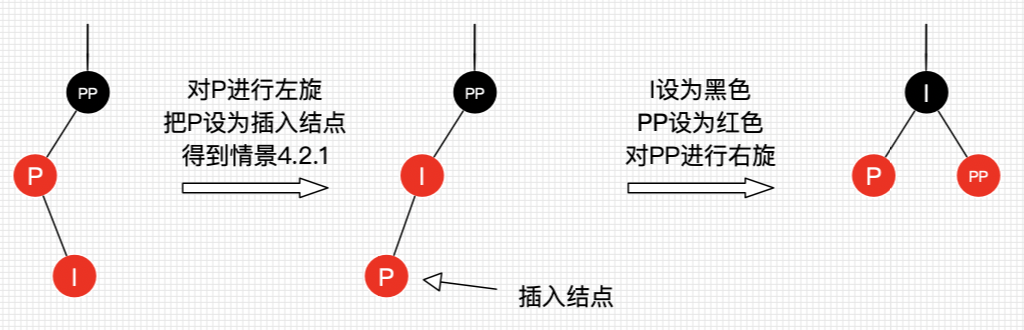
红黑树的删除

删除主要分为三个步骤：

  • 找到待删除的节点
  • 找替代节点
  • 替代后调整平衡

替代节点也有三种情形：

  • 若删除结点无子结点，直接删除

  • 若删除结点只有一个子结点，用子结点替换删除结点

  • 若删除结点有两个子结点，用后继结点（大于删除结点的最小结点）替换删除结点

下图就很形象的说明了什么叫后继节点。

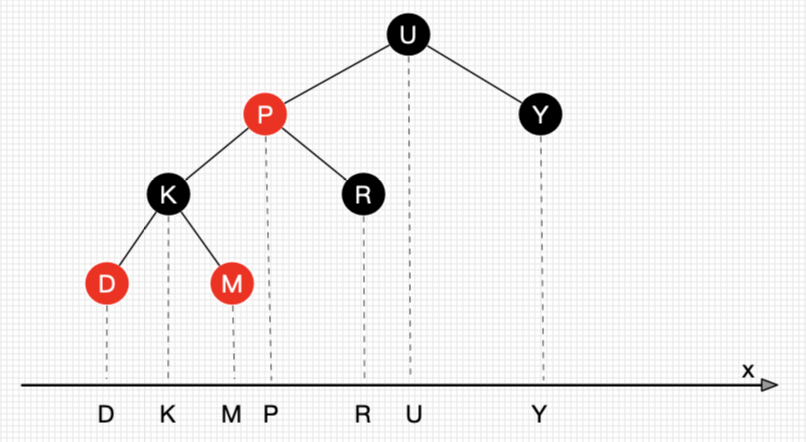
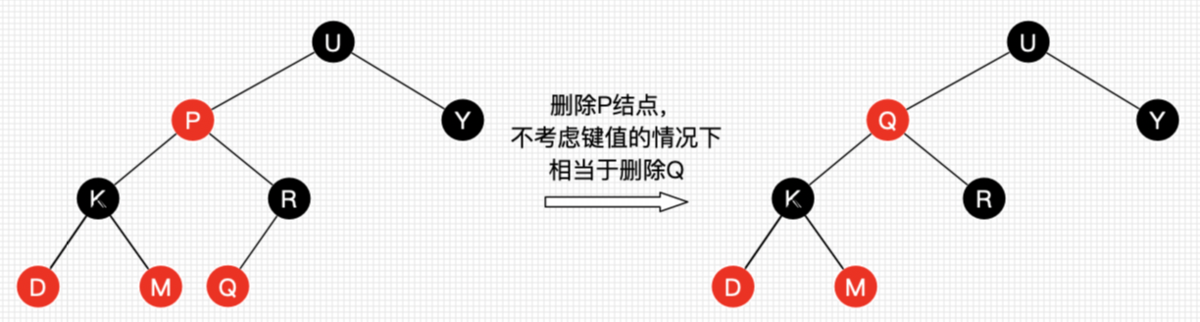
一个很重要的观点

删除结点被替代后，在不考虑结点的键值的情况下，对于树来说，可以认为删除的是替代结点！

节点命名规则

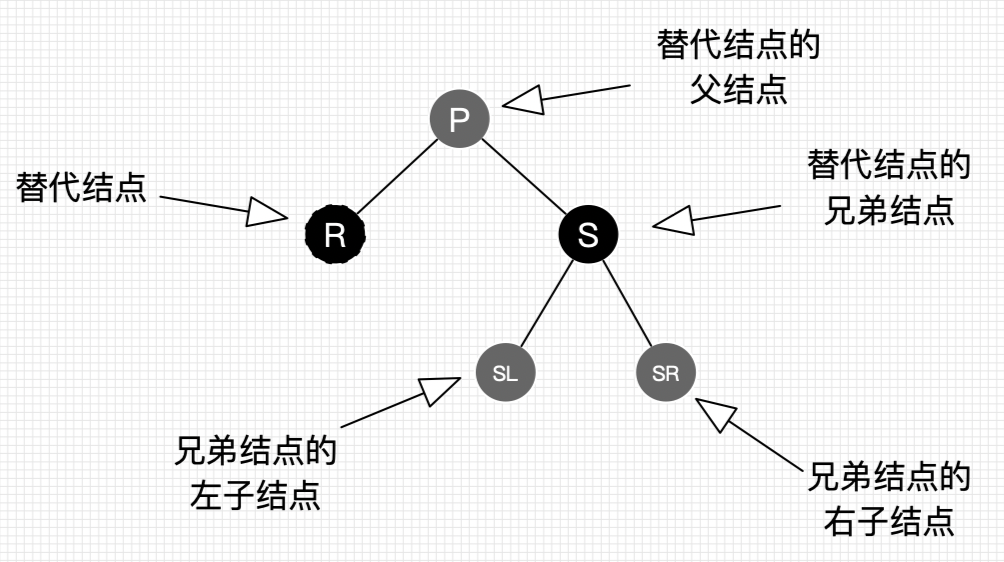
情景1: 替代节点是红节点

由于替换结点时红色，删除（这个是之前那个重要观点）也了不会影响红黑树的平衡，只要【把替换结点的颜色设为删除的结点的颜色】即可重新平衡。

情景2: 替换节点是黑色

根据那个重要观点，这个时候相当于删除了一个黑色节点，会影响整棵树的黑高。故需要调整。

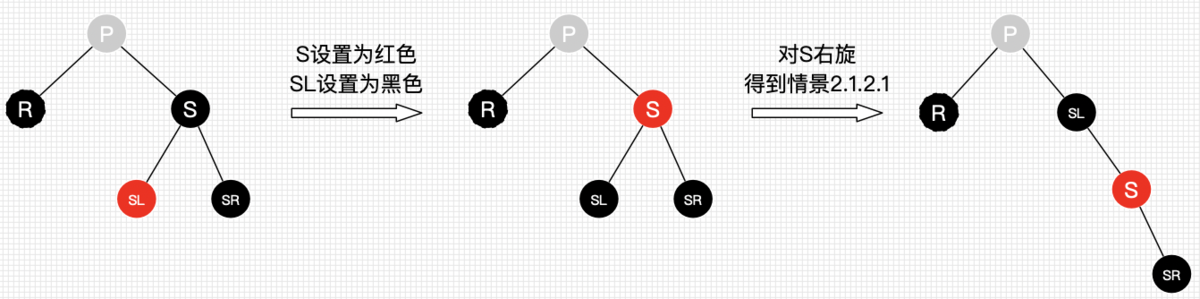
情景2-1: 替换节点的兄弟节点是红节点

这个时候我们删除了左子树的一个黑色结点，显然左子树的黑色结点少1了，然而右子树又是红色结点，那么我们直接向右子树“借”个红结点来补充黑结点。

情景2-2: 替换节点的兄弟节点是黑节点

2-2-1: 替换结点的兄弟结点的子节点有红色的

这个时候和2-1很像，我们在左子树删除了一个黑色节点，右子树又有红色节点，我们可以向右子树“借”红色节点。

2-2-2：替换节点的兄弟节点都是黑的

这个时候兄弟子树已经帮不上忙了，只能自底向上考虑，靠父节点了。

我们把当前替换节点的兄弟节点设成红色，然后把替换节点修改成父节点。然后再重新处理。

删除节点在右侧的情形一样，我就不赘述了。