本篇文章极大地参考了博客

背景

在商品推荐领域常用的方法有矩阵分解（Matrix Factorization）和最近邻搜索（kNN）等。但是这两种方法都没有针对推荐排序问题的优化方法，因此本文提出一个关于针对个性化推荐排序问题的优化方法——BPR-OPT，并将其应用到MF和kNN方法之中。

问题建模

我们用 $U$ 表示所有 $user$ 的集合，$I$ 表示所有 $item$ 的集合。$S \subseteq U \times I$ 表示所有隐式反馈的合集。$>_u \subset I^2$ 表示用户 $u$ 对物品的偏好关系，比如 $i >_u j$ 表示用户 $u$ 更喜欢 $i$

我们记：

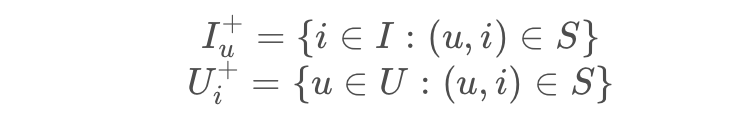
接下来我们要做的就是把用户与物品之间的隐式反馈转化成矩阵，以此进行数据处理。一般表现为0-1矩阵，即 $user$ 和 $item$ 有交互对应位置为1，否则为0。

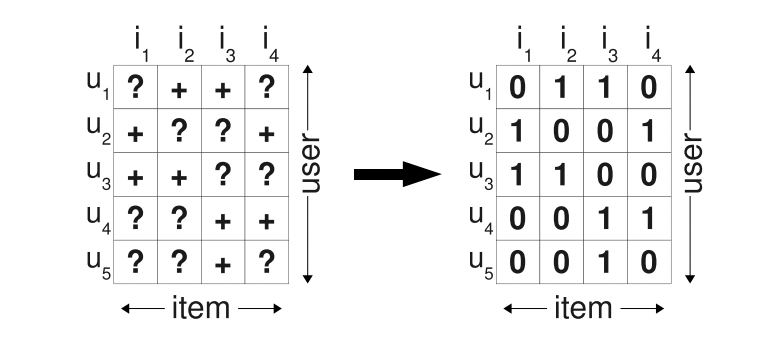
我们的任务是：根据现有的矩阵，预测没有交互的 $user-item$ 的分数，分数越高表示偏好程度越高，然后排序进行推荐。

在BPR算法中，它的核心是偏序关系三元组，即我们有：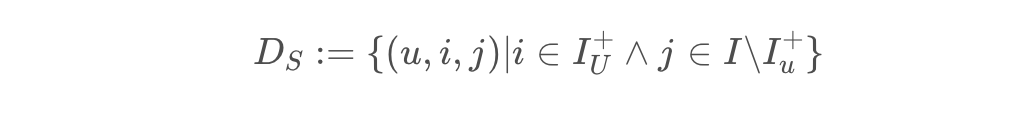

$(u,i,j)$ 表示对于用户 $u$ 来说，喜欢物品 $i$ 的程度要高于物品 $j$ ，我们可以对原始矩阵再进行转换变成下面的矩阵，得到特定用户对于两个物品的偏序关系矩阵。

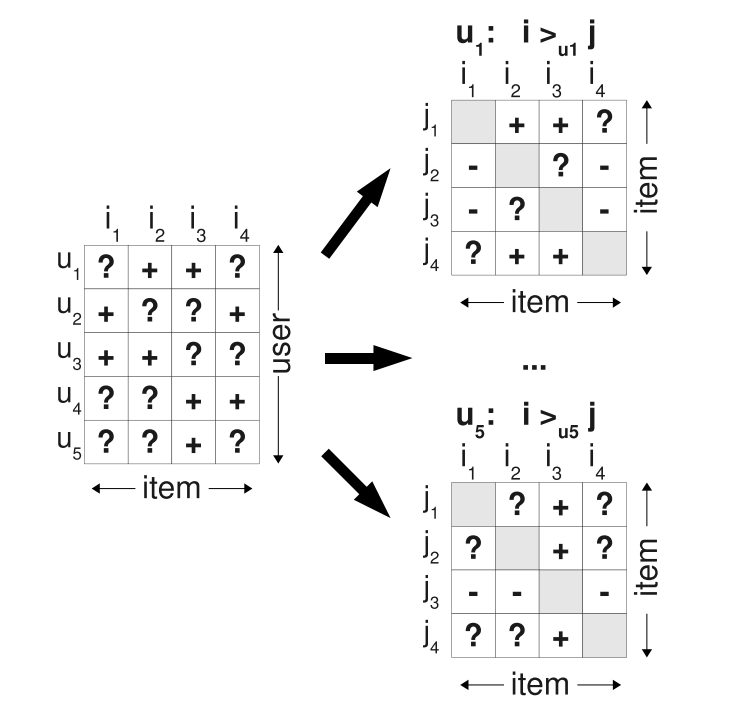
所以我们每次修正的时候不是修正 $u$ 对一个物品的评分而是对两个物品的评分。

贝叶斯公式：

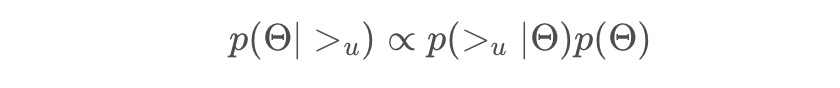
$\theta$ 代表一个任意的模型类的参数向量.

我们先处理 $p(>_u|\theta)$

我们有以下两个假设：

那么对于任意一个用户u来说，$p(>_u)$ 对所有的物品一样，我们可以得到

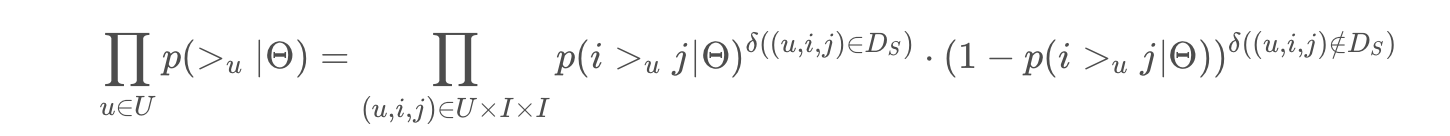
对于每个 $user$ ，给定商品对 $(i,j)$ ，其关系有四种：

	i是正样本	i是未观测的样本
j是正样本	0	0
j是未观测的样本	1	0

所以上面的式子可以化简为：

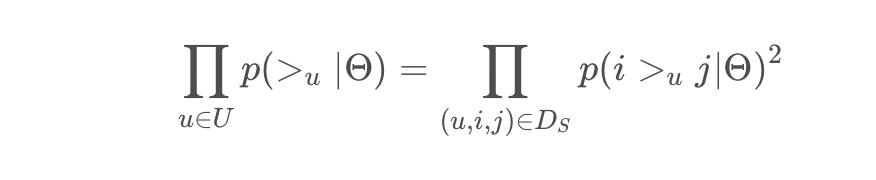
根据非负性我们可以把平方去掉，得到论文里的公式

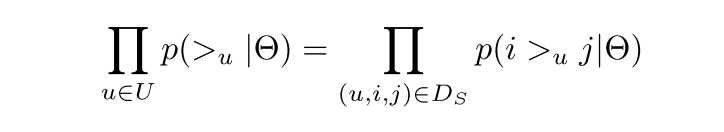
我们定义：

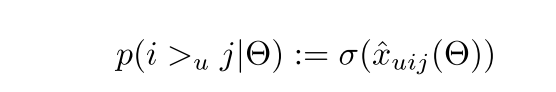
其中 $\widehat{x}_{uij}$ 为为模型对用户u对 i 和 j 相对的打分

再处理 $p(\theta)$

原作者大胆使用了贝叶斯假设，即这个概率分布符合正太分布，且对应的均值是0，协方差矩阵是 $\sum_{\theta}$

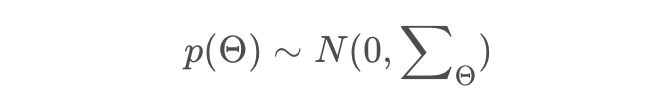
我们令 $\sum_{\theta} = \lambda_\theta I$，那么原先的优化问题就转换为

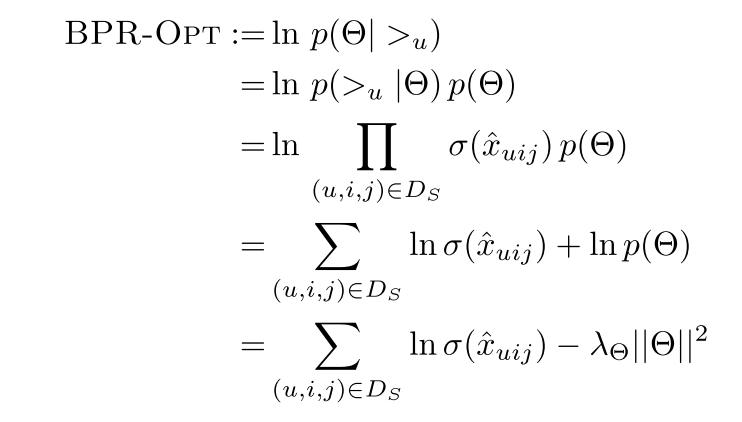
其中 $\lambda_\theta||\theta||^2$ 就是正则化系数。根据上面提出的BPR-OPT指标，我们采用梯度下降的算法。对BPR-OPT指标求导：

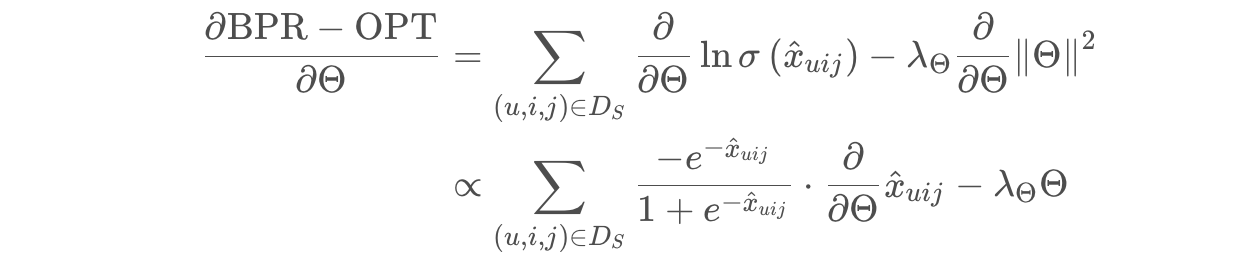
AUC指标：