私有数据检索PIR
定义
私有信息检索(Private Information Retrieval, PIR)的问题描述是:服务器Bob拥有一个数据库,其中有n个数据 $d_1,d_2,…,d_n$,客户端Alice要查询这个数据库的某条数据$d_i$,而Bob却不知道$i$的值。
如果我们对服务器的数据隐私也进行保护,即Alice除了$d_i$ 得不到任何其他信息,这就是对称的私有信息检索(Symmetrically-Private Information Retrieval,SPIR)。
最简单的方法
我们假设服务器储存的是一串字符串。Bob直接把这一串数据发给Alice,然后Alice直接选取需要的字符。但是这种方法显然不适用大数据的情况。
PIR[CGKS95]
来自论文[1],我们需要两个存有相同数据(比如图中的$ABCDEFGHI$)的Server。
- User需要创造两个集合,一个集合包含我们需要检索的数据序号$i$,另一个不包含。
- 将两个集合发给两个服务器,服务器将对应序号的数据进行异或求和,最终得到1-bit查询结果(图中是B^E^G,和B^C^E^G)。
- User再将两个查询结果进行异或,就能得到需要的数据了。
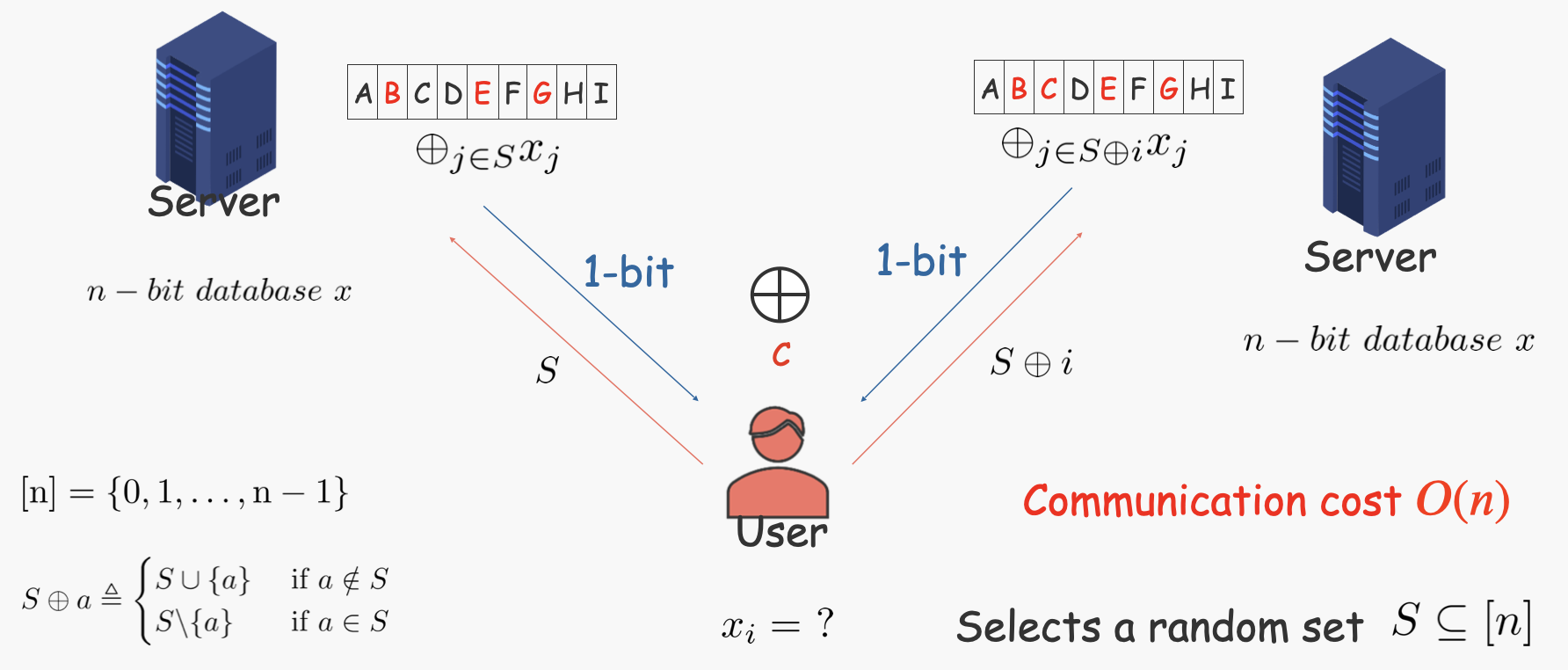
假设Server存储的数据长度为$n$,User给某个Server发的集合长度为$m$,为了使Server猜对User检索哪个数据的概率为$1/n$,则$m$需要满足:
1/2表示Server要猜测检索的数据在不在User发给自己的集合里(⚠️这句话要理解一下)。
可见这个方法的 Communication cost 为 O(n)。
改进
将Server中的数据存成多维矩阵的形式。以二维为例,User发送的集合将变成二维坐标形式$(S_1, S_2)$
同时,我们发现如果还是两个Server的话,计算结果并不正确。我们需要将Server增加到4个。
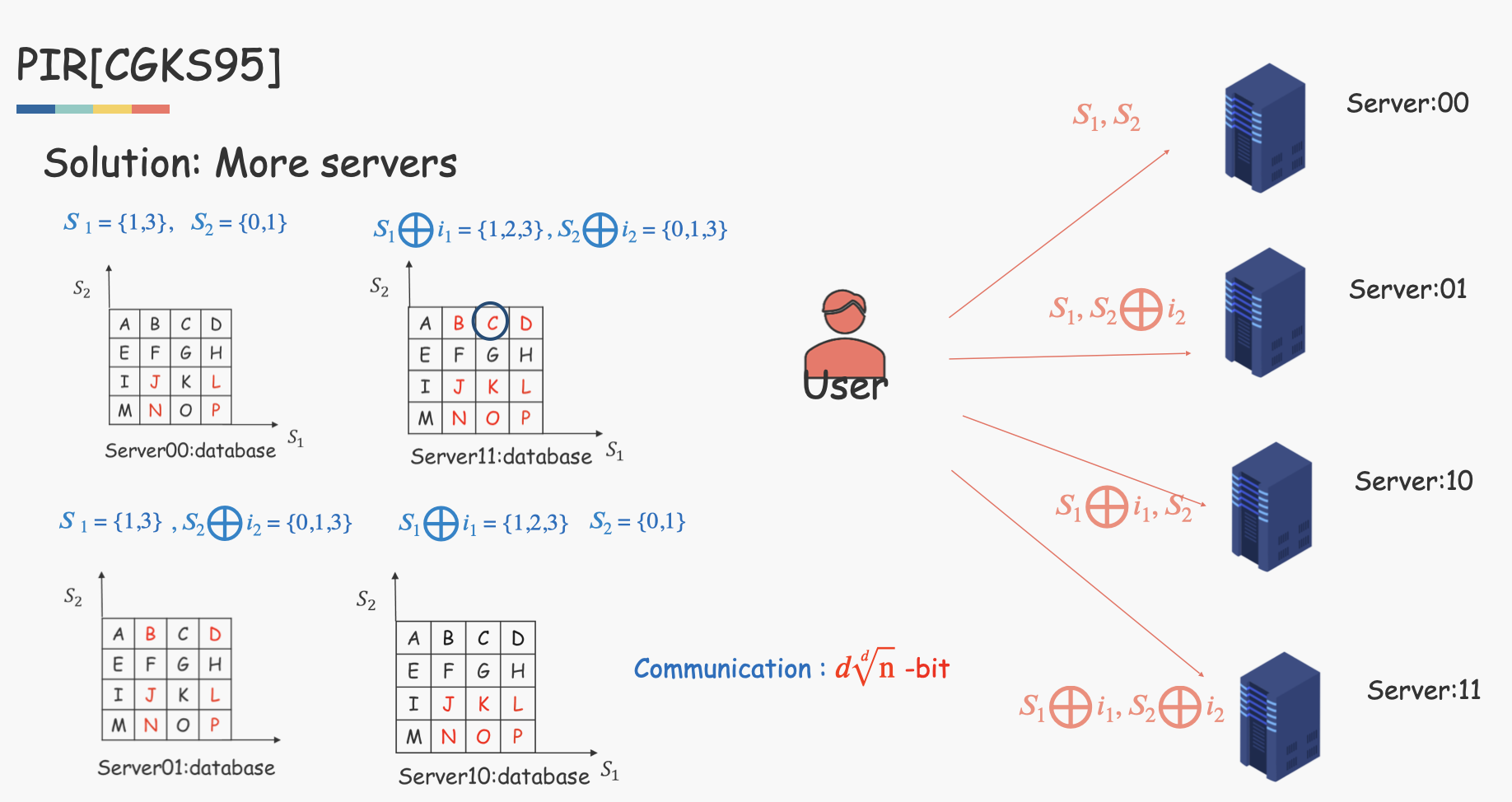
这种方法通过多个数据库副本实现的PIR的研究方法称作是Information- Theoretic Private Information Retrieval(IPIR,信息论私有信息检索)。IPIR 具有信息论意义上的安全性,但通信复杂度和存储复杂度太高(需要这么多服务器!)。如果用户只要求计算意义上的隐私保护,可以只使用一个服务器。
cPIR[CG97]
来自论文[2],假设Server只有多项式的算力,那么可以借助一些密码学的假设实现1个Server情况下的PIR。
KO97
来自论文[3],基于半同态加密。同态加密满足下面两个公式。
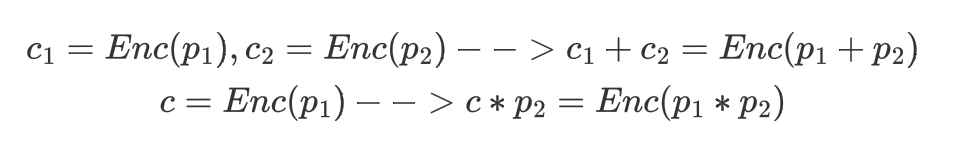
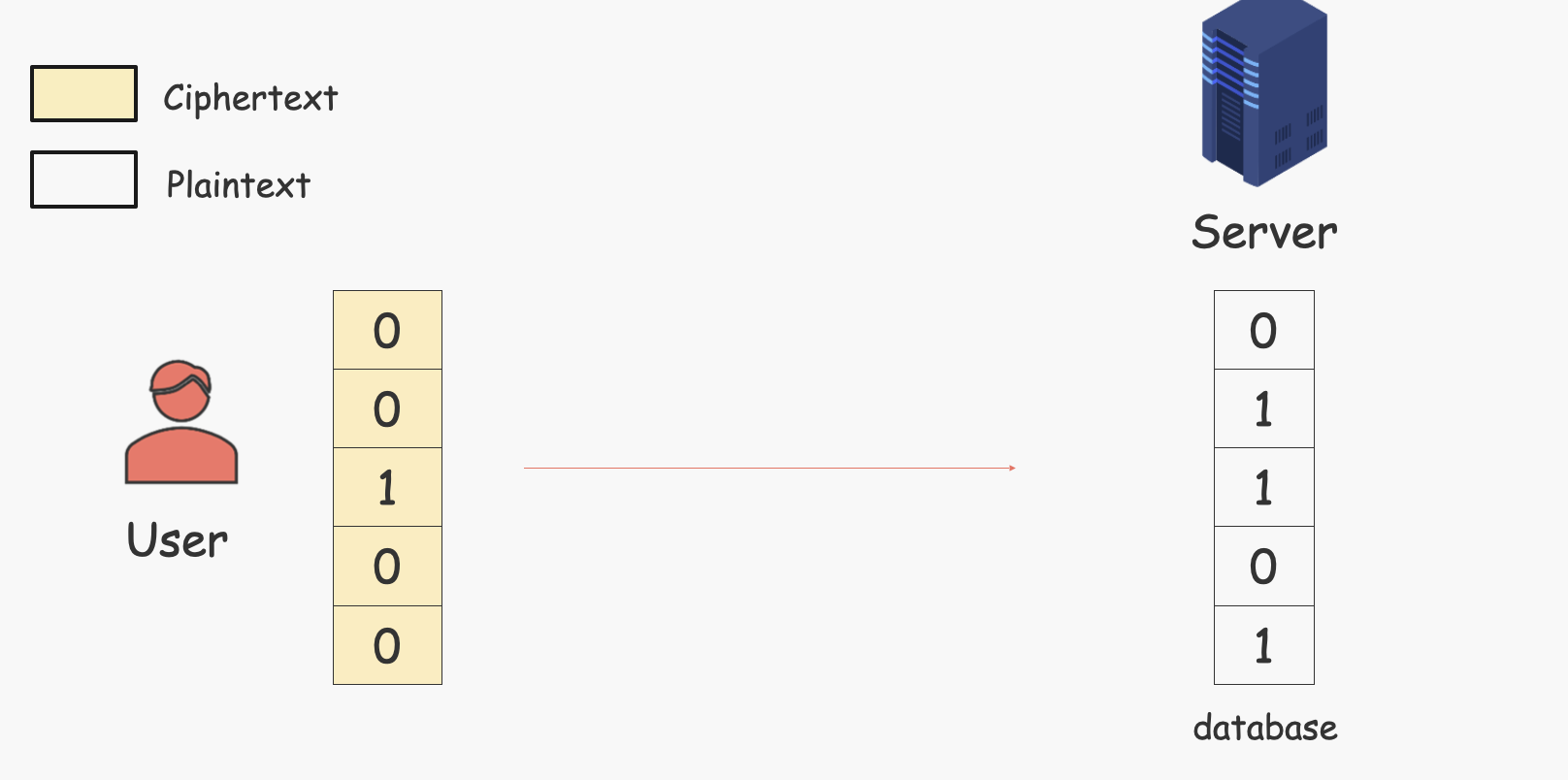
- 首先User还是需要生成一个选择向量(比如图中选择的是第三个数据),然后对这个向量进行同态加密(⚠️图中黄色部分是加密后的数据,也就是外人看上去就是一团乱码,每个数据都不一样)。
- 然后将数据库里的数据与这个向量相乘(就是上面的第二个公式),将结果相加(第一个公式,但是由于我们先乘了,所以这里得到的结果就是$Enc(d_i)$)。
- 然后User再对结果解密,就可以得到需要的数据。
优化方式也是变成多维。
Gentry09
来自论文[4],基于全同态加密。满足下面的公式
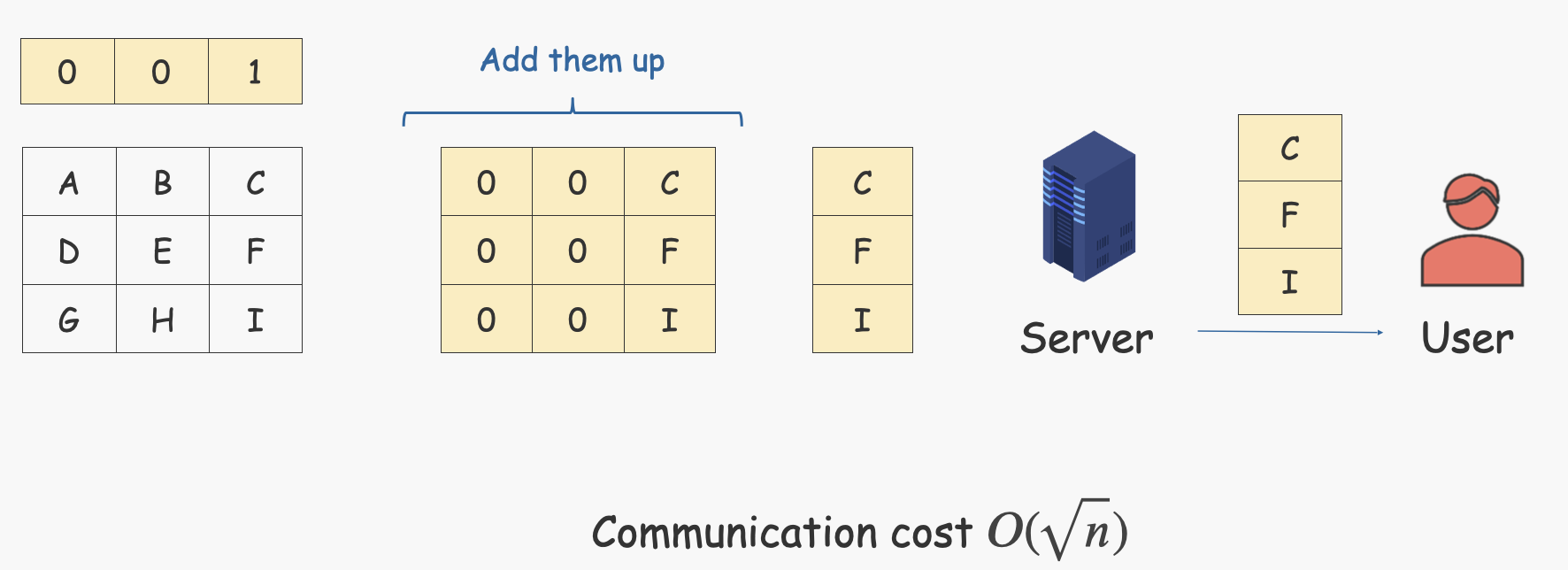
首先User生成一个选择向量(比如00000100,我们需要选取序号为5的数据)
对这个序号进行一次“重排”(比如我们上面的向量只有8位,所以数据库的数据只有8个,我们只需要3位二进制数就可以表示了,那么这里我们00000100 -> 101)
然后对序号取反(101 -> 010),按位加密再发给服务器($Enc(0)Enc(1)Enc(0)$)。
Server将对应的序号与User发送的信息按位相加(相加结果与选择的同态算法有关,这里我们假设mod2)
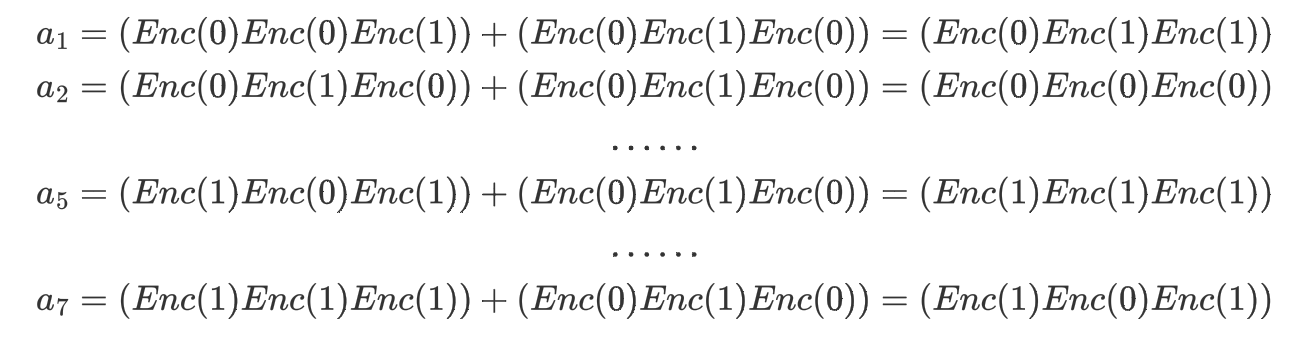
然后将结果按位乘
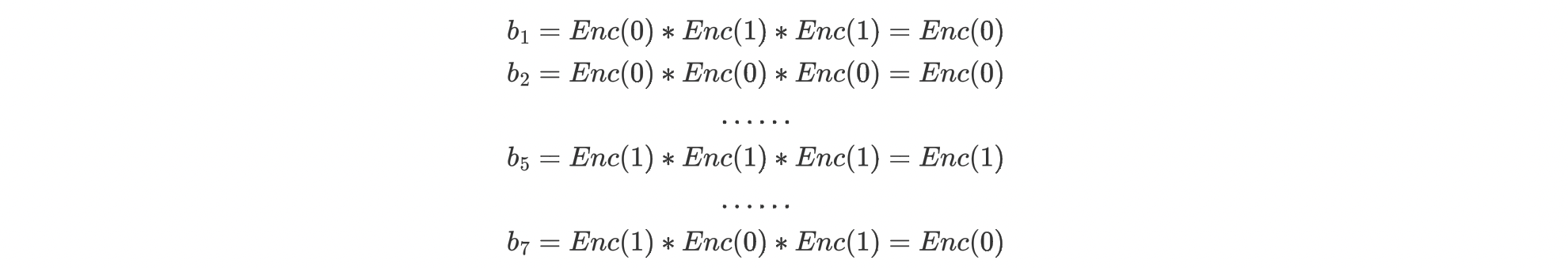
然后把乘法的结果求和发给User,User解密就得到了数据。
⚠️ 这里的运算都是同态加密后的运算,其实是一堆乱码在计算。
但是这个方法虽然减小了通信量(原来发8位数字,现在发log8=3位),但是计算量加大了。
优化 SealPIR [ACLS2017]
优化的思路就是优化Gentry09在Sever端的计算步骤[5],User只要把加密后的序号发给Server,Server就能高效地扩展出选择向量。
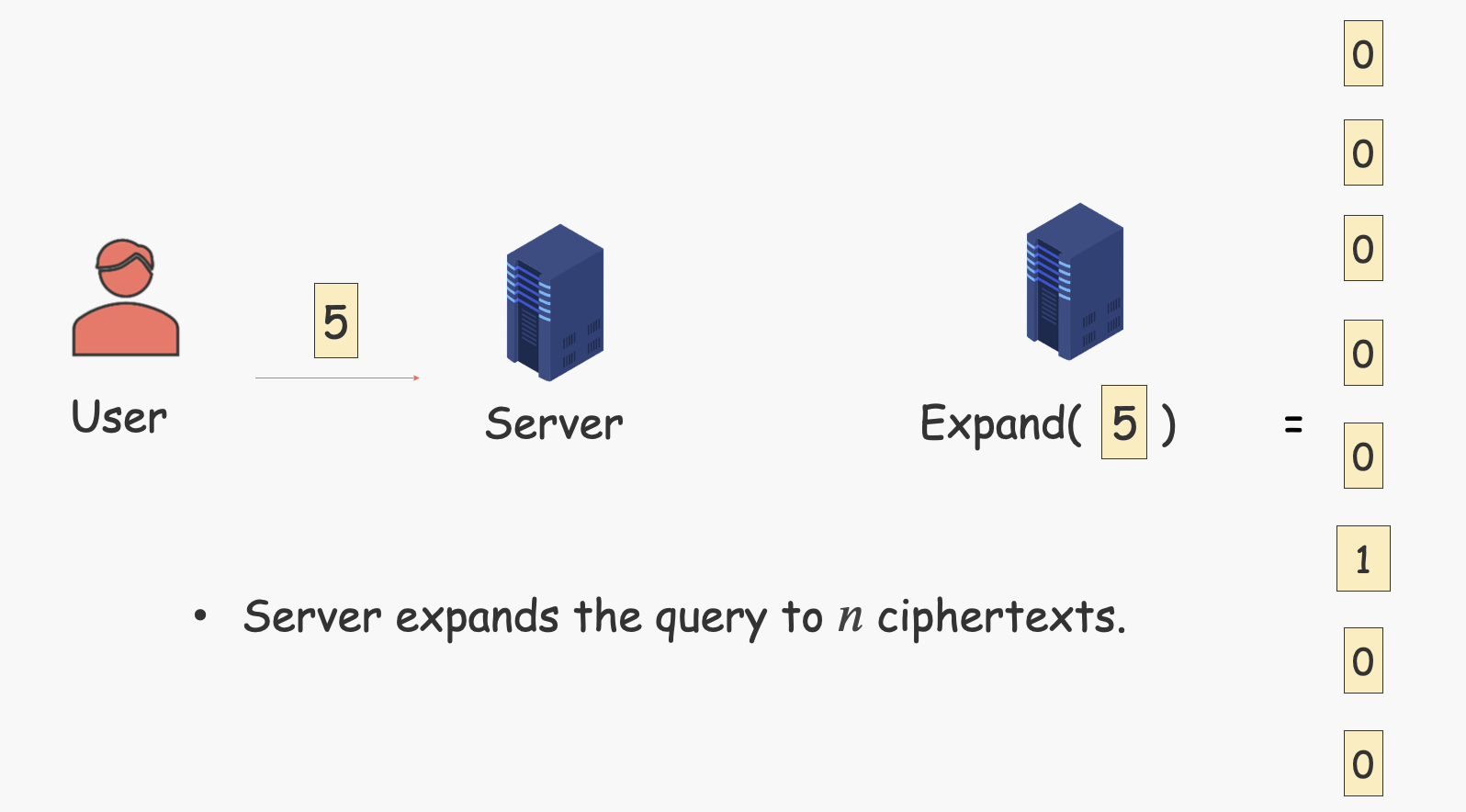
这个时候我们的全同态算法需要构造出一个新的特性:
这里$c$是密文,$p(x)$是明文,$Sub$的第二个参数是奇数。这个算法规定模是$x^N+1$。那么我们可以知道如果计算$x^N$取模得到的结果是$-1$,$x^{N+1}$得到的是$-x$。$N$是数据的长度,$x$是一个常数。即:
具体的扩展步骤为(假设User选择序号为5的数据,即发送给Server的是$Enc(5)$):
Server先做$c_j = Enc(x^{i-j})$
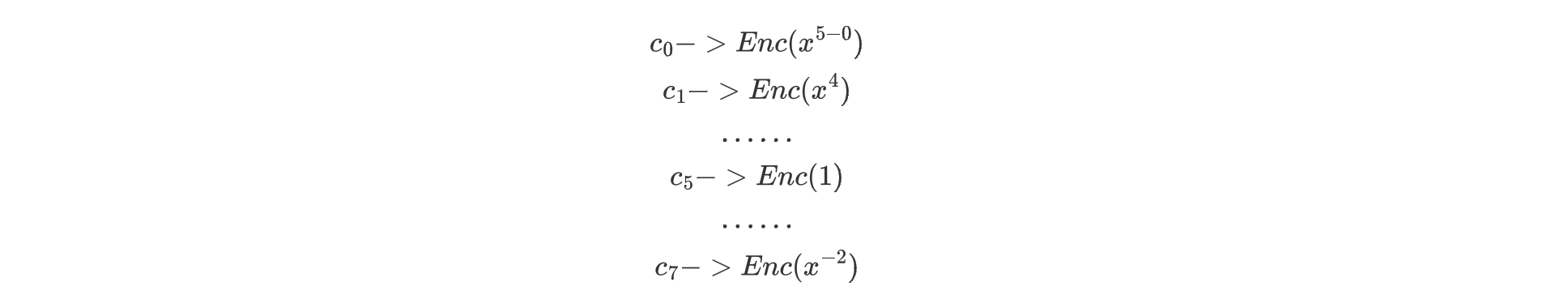
然后进行$Sub(c_j,N+1)$
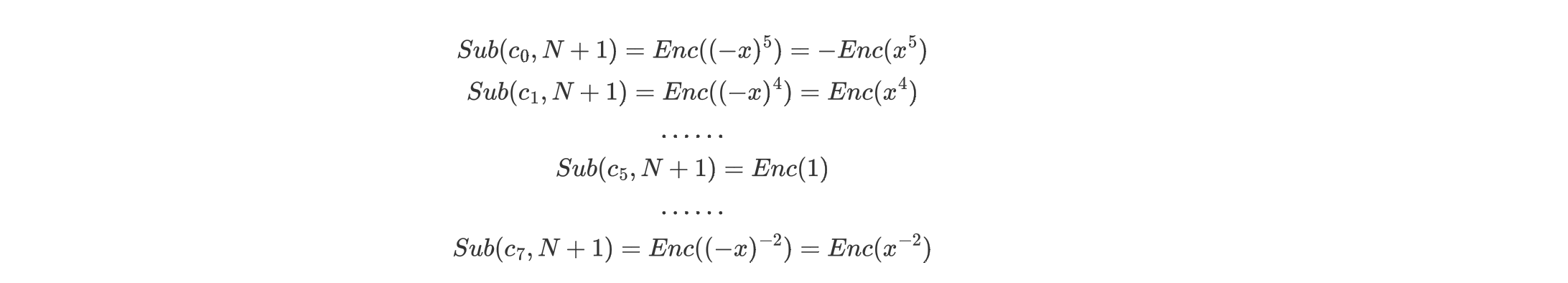
然后执行$f(x) = c_j+Sub(c_j,N+1)$,这一步其实就是消去奇数项,偶数项和我们选择的那项都翻倍。
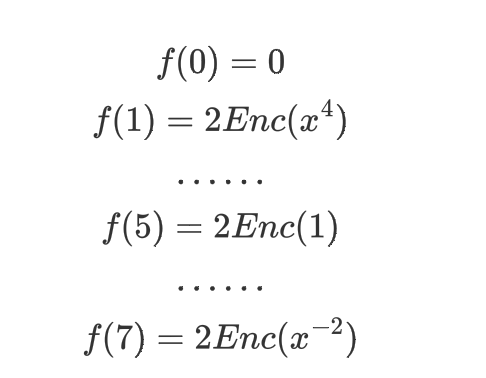
然后我们把剩下的做$c_j = c_j * x^{\frac{1}{2}}$,这样又回生成一部分指数是奇数的项,然后重新执行第一步。最后只有User选择的没有被消掉。当然其实Server是不知道那些是消掉那些是剩下的,只是对消掉的做上述步骤其值还是0.
这样只要重复logN次就可以得到Gentry09里面最后的向量$\{Enc(0),Enc(0),…,Enc(1),…,Enc(0)\}$。
PPY18
上课没讲
【1】Chor, B., Goldreich, O., Kushilevitz, E., & Sudan, M. (1995, October). Private information retrieval. In Proceedings of IEEE 36th Annual Foundations of Computer Science (pp. 41-50). IEEE.
【2】Chor, B., & Gilboa, N. (1997, May). Computationally private information retrieval. In Proceedings of the twenty-ninth annual ACM symposium on Theory of computing (pp. 304-313).
【3】Kushilevitz, E., & Ostrovsky, R. (1997, October). Replication is not needed: Single database, computationally-private information retrieval. In Proceedings 38th annual symposium on foundations of computer science (pp. 364-373). IEEE.
【4】Gentry, C. (2009, May). Fully homomorphic encryption using ideal lattices. In Proceedings of the forty-first annual ACM symposium on Theory of computing (pp. 169-178).
