加密数据库Encrypted Database
超几何分布
假设有 $N$ 个球,其中黑球 $M$ 个,白球 $N−M$ 个,每次不放回、随机地抽取一个球。那么在抽取总共 $y$ 个球的情况下有多少个黑球是一个随机变量。我们用$X$来表示这个随机变量,用$x$表示具体的黑球数量,那么满足 $X=x$ 的概率是
BCLO
BCLO[1]是一种保序加密,即加密后的数据顺序与加密前的一样,即对于$y_i = Enc(x_i)$,我们有 $\forall i,j, x_i>x_j \Leftrightarrow y_i>y_j$
同时BCLO还满足以下条件:
- 支持便利地加解密,支持插入数据更新数据库
- 只需要O(1)的储存复杂度
BCLO是基于超几何分布(Hypergeometric distribution,HG)的:
假如有明文域 $M$ 和密文域 $N$,$N>M$,从密文域 $N$ 中随机抽取 $M$ 个不同的整数组成有序集合 $S$ ,构造了一个保序函数 $f$,把第 $i$ 个明文 $m$ 映射到第 $i$ 个密文$c$,那么一个保序函数 $f$ 对应唯一的组合 $C^M_N$。
算法描述

举个例子,我们要把 [1, 100] 这个区间的整数映射到 [1, 1000] 中,我们采用上述方法映射一个数字,我们先选择25进行映射(即我们要加密25)。
我们直接看第11行,它的意思是:我们从一个框里面抽球,里面黑球有 $M$ 个(就是明文域的大小100),白球有 $N$ 个(就是密文域的大小1000),我抽了 $y$个球(就是密文域大小的一半500),这个 $HG()$函数可以给我返回我抽了多少个黑球,也就是数值 $x$(这个值必然是0-100之间的数,因为我从1100个球里面抽,可能抽不到黑球,也可能抽到所有的黑球)。
接下来,阐述具体的超几何采样的步骤:
- 假设我采样到了44这个数,因为大于25,所以重新调整明文域和密文域分别为[1, 44],[1, 500];反之,如果我抽到的数小于25,假设是11,那么分别调整为[11, 100],[500,1000]。
- 调整后,继续进行上述抽球活动。就这样反复抽几轮,一定能抽到明文域里的25,密文域也在一半一半的切,至于切左区间还是右区间,要看每次抽样抽到的 $x$ 与25的大小关系,最后从区间[283, 298]的区间中随机取一个数作为25的密文。⚠️:不仅要抽样,还要把每次抽样结果记录在key_table这张表里面!因为这样做在加密下一个数(比如26)可以查表从299开始,起到了加速作用
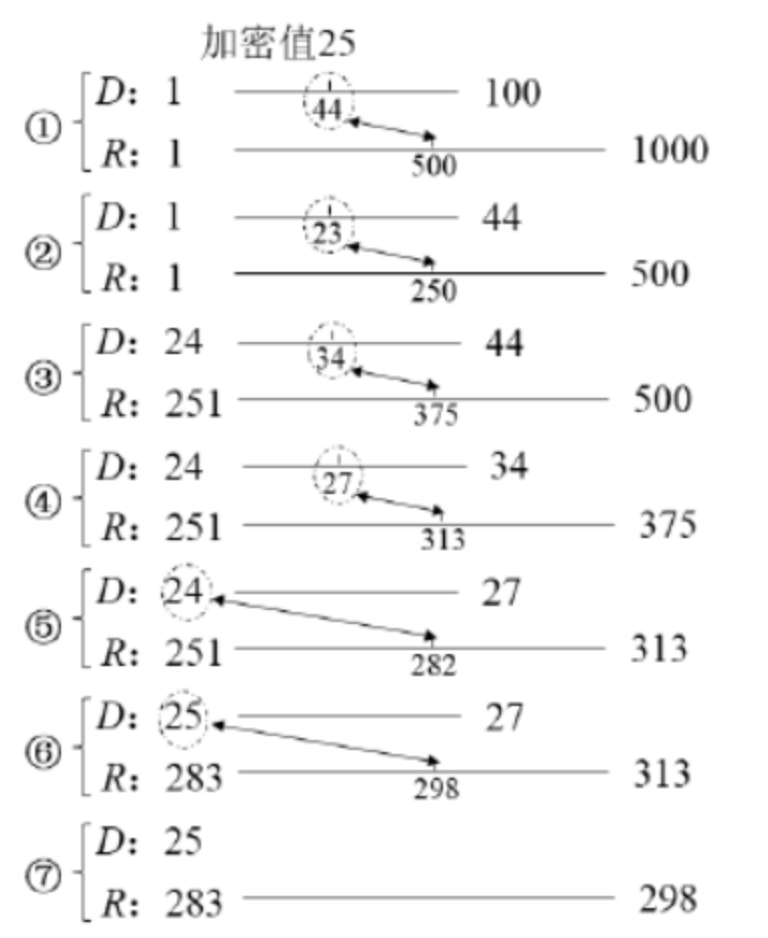
解密操作就是上述的逆过程。每次一递归过程中,密文域总是被缩短一半。所以这个算法的时间复杂度最差情况下是 $logN+1$,平均情况是 $5logM+12$。相关的时间复杂度证明请参见Boldyreva的论文。
插入
直接对待插入的数据进行加密,然后发给Server进行更新就好了。
数据库的范围查询(range query)
假设我们要查询小于10的数,我们只要返回
缺点
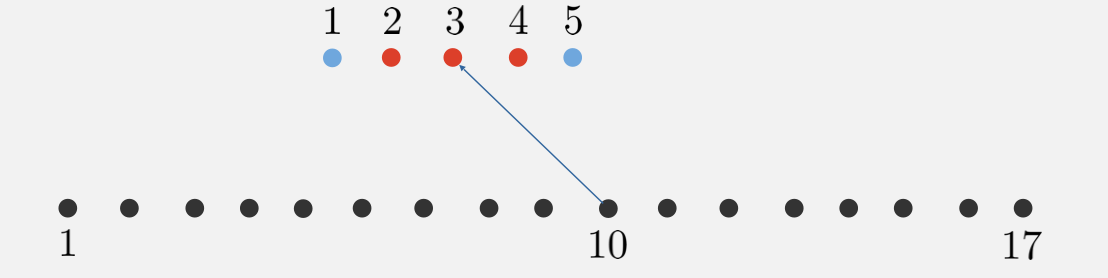
会泄露一半长度的信息并且明文之间的距离也会被泄露。比如我们知道两端的节点映射情况1->1,5->17.中间有个节点10,那对应的明文必然是2,3,4中的一个。
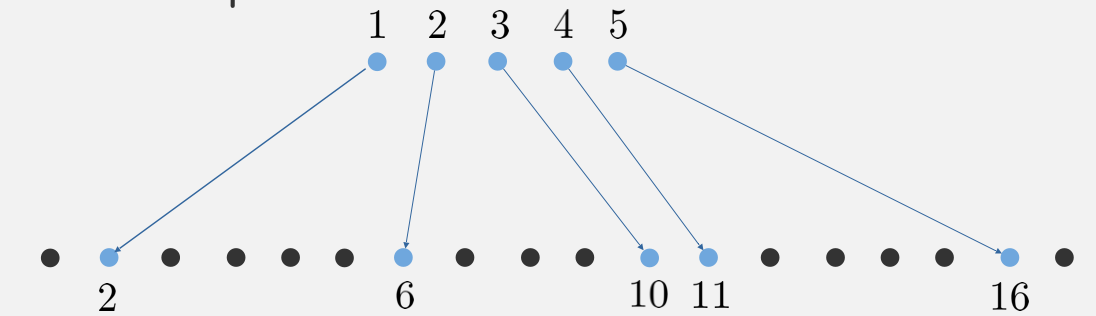
明文距离泄露的情况。比如给定密文(10,11),我们可以推测是(3,4)而不会推测是(3,5)
Modular OPE
为了避免泄露一半的信息,BCLO的作者提出了Modular OPE[4]。将映射好的顺序做一定的旋转。

参考
【1】Boldyreva, A., Chenette, N., Lee, Y., & O’neill, A. (2009, April). Order-preserving symmetric encryption. In Annual International Conference on the Theory and Applications of Cryptographic Techniques (pp. 224-241). Springer, Berlin, Heidelberg.
【2】https://blog.alienx.cn/2019/11/07/E11071745/
【3】https://blog.csdn.net/qq_37150711/article/details/111348696
【4】Boldyreva, A., Chenette, N., Lee, Y., & O’neill, A. (2009, April). Order-preserving symmetric encryption. In Annual International Conference on the Theory and Applications of Cryptographic Techniques (pp. 224-241). Springer, Berlin, Heidelberg.
